Phương pháp giải:

+) Gọi G là trọng tâm tam giác ABC \( \Rightarrow SG \bot \left( {ABC} \right)\).

+) Tính diện tích tam giác đều ABC theo b và h.

+) Sử dụng công thức tính thể tích khối chóp \({V_{S.ABC}} = \dfrac{1}{3}SG.{S_{ABC}}\).

Lời giải chi tiết:

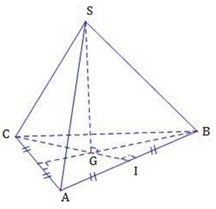
Gọi G là trọng tâm tam giác ABC \( \Rightarrow SG \bot \left( {ABC} \right)\).

Tam giác SCG vuông tại G \( \Rightarrow CG = \sqrt {S{C^2} - S{G^2}}  = \sqrt {{b^2} - {h^2}} \)

\(\begin{array}{l} \Rightarrow CI = \dfrac{3}{2}CG = \dfrac{3}{2}.\sqrt {{b^2} - {h^2}} \,\,\\ \Rightarrow AI = CI.\tan {30^0} = \dfrac{{\dfrac{3}{2}.\sqrt {{b^2} - {h^2}} }}{{\sqrt 3 }} = \dfrac{{\sqrt 3 }}{2}.\sqrt {{b^2} - {h^2}} \,\, \Rightarrow AB = \sqrt 3 .\sqrt {{b^2} - {h^2}} \,\,\\ \Rightarrow {S_{ABC}} = \dfrac{1}{2}.CI.AB = \dfrac{1}{2}.\dfrac{3}{2}\sqrt {{b^2} - {h^2}} .\sqrt 3 .\sqrt {{b^2} - {h^2}} \,\, = \dfrac{{3\sqrt 3 }}{4}\left( {{b^2} - {h^2}} \right)\end{array}\)

Thể tích của khối chóp là: \({V_{S.ABC}} = \dfrac{1}{3}.SG.{S_{ABC}} = \dfrac{1}{3}.h.\dfrac{{3\sqrt 3 }}{4}\left( {{b^2} - {h^2}} \right) = \dfrac{{\sqrt 3 }}{4}\left( {{b^2} - {h^2}} \right)h\)

Chọn: A