Phương pháp giải:

Sử dụng công thức tính thể tích chóp \({V_{chop}} = \dfrac{1}{3}{S_{day}}.h\).

Lời giải chi tiết:

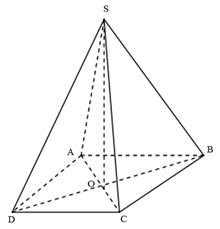
Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\).

Diện tích đáy: \({S_d} = A{B^2} = {6^2} = 36\)

ABCD là hình vuông tâm O \( \Rightarrow OB = \dfrac{{AB}}{{\sqrt 2 }} = \dfrac{6}{{\sqrt 2 }} = 3\sqrt 2 \)

Tam giác SOB vuông tại O

\( \Rightarrow SO = \sqrt {S{B^2} - O{B^2}}  = \sqrt {{6^2} - {{\left( {3\sqrt 2 } \right)}^2}}  = \sqrt {36 - 18}  = 3\sqrt 2 \)

Thể tích khối chóp: \({V_{S.ABCD}} = \dfrac{1}{3}.SO.{S_d} = \dfrac{1}{3}.3\sqrt 2 .36 = 36\sqrt 2  \approx 51\).

Chọn: D