Câu hỏi
Thiết diện qua trục của một hình nón là một tam giác đều cạnh có độ dài 2a. Thể tích của khối nón là:
- A \(\dfrac{{\pi {a^3}\sqrt 3 }}{6}\).
- B \(\dfrac{{\pi {a^3}\sqrt 3 }}{3}\).
- C \(\dfrac{{\pi {a^3}\sqrt 3 }}{2}\).
- D \(\dfrac{{\pi {a^3}\sqrt 3 }}{{12}}\).
Phương pháp giải:
Thể tích khối nón: \(V = \dfrac{1}{3}\pi {R^2}h\).
Lời giải chi tiết:
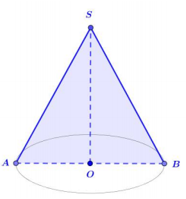
Giả sử hình nón có đỉnh S, tâm đáy là O, thiết diện qua trục là SAB.
Ta có: tam giác\(SAB\) đều cạnh 2a \( \Rightarrow R = a\)
Tam giác \(SOA\) vuông tại \(O\) có: \(h = SO = \sqrt {S{A^2} - A{O^2}} = \sqrt 3 a\)
Thể tích khối nón là: \(V = \dfrac{1}{3}h\pi {R^2} = \dfrac{1}{3}.\sqrt 3 a.\pi {a^2} = \dfrac{{\sqrt 3 \pi {a^3}}}{3}\).
Chọn: B
Câu hỏi trước
