Câu hỏi
Một vật có khối lượng m = 10kg đang đứng yên trên mặt phẳng nằm ngang. Biết hệ số ma sát trượt giữa vật và sàn là μ = 0,1. Lấy g =10m/s2. Tác dụng một lực kéo F =30N theo phương ngang vào vật.
a, Xác định gia tốc và vận tốc của vật sau 5 giây.
b, Sau 5 giây thì lực F ngừng tác dụng. Xác định thời gian và quãng đường mà vật đi được kể từ khi lực F ngừng tác dụng.
c, Sau 5 giây kể từ khi vật bắt đầu chuyển động, tác dụng thêm lực F1 = 45N vào vật và có hướng ngược với hướng chuyển động của vật. Xác định quãng đường mà vật đi được trong 5 giây kể từ khi có thêm lực F1
Phương pháp giải:
Động lực học chất điểm
Lời giải chi tiết:
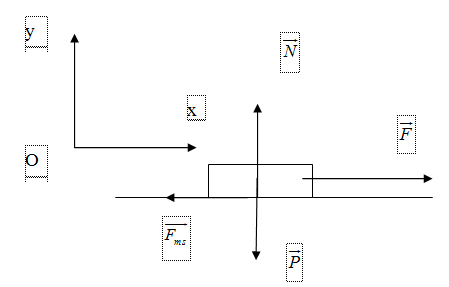
Ta có hình vẽ:
Chọn hệ trục tọa độ Oxy như hình .
Các lực tác dụng vào vật gồm :
\(\overrightarrow N ,\overrightarrow P ,\overrightarrow F ,\overrightarrow {{F_{ms}}} \)
Áp dụng định luật II Niu- tơn.
\(\overrightarrow N + \overrightarrow P + \overrightarrow F + \overrightarrow {{F_{ms}}} = m.\overrightarrow a \)
Chiếu lên hai trục Ox và Oy ta có:
\(\begin{array}{l}
{\rm{Oy: N - P}} = 0 \Leftrightarrow N = P = mg\\
{\rm{Ox: F - }}{{\rm{F}}_{ms}} = m.a \Leftrightarrow F - \mu N = ma\\
= > a = \frac{{F - \mu N}}{m} = \frac{{F - \mu .m.g}}{m} = \frac{{30 - 0,1.10.10}}{{10}} = 2m/{s^2}
\end{array}\)
Phương trình vận tốc là: v = v0 + at = at => v5 = 2.5 = 10 m/s2
b) Khi ngừng tác dụng lực thì các lực tác dụng lên vật là
\(\overrightarrow N ,\overrightarrow P ,\overrightarrow {{F_{ms}}} \)
Áp dụng định luật II Niu- tơn.
\(\overrightarrow N + \overrightarrow P + \overrightarrow {{F_{ms}}} = m.\overrightarrow {a'} \)
Chiếu lên hai trục Ox và Oy ta có:
\(\begin{array}{l}
{\rm{Oy: N - P}} = 0 \Leftrightarrow N = P = mg\\
{\rm{Ox: - }}{{\rm{F}}_{ms}} = m.a' \Leftrightarrow - \mu N = ma'\\
= > a' = \frac{{ - \mu N}}{m} = \frac{{ - \mu .m.g}}{m} = \frac{{ - 0,1.10.10}}{{10}} = - 1m/{s^2}
\end{array}\)
Vậy từ sau 5s thì vật chuyển động chậm dần đều với gia tốc – 1 m/s2
Phương trình vận tốc là v = v5 + a’t = 10 – t
Đến khi vật dừng lại thì v = 0 nên ta có: 10 – t = 0 => t = 10s
Áp dụng công thức độc lập với thời gian ta có: v2 – v52 = 2.a’.s
=> \(s = \frac{{0 - {{10}^2}}}{{2.( - 1)}} = 50m\)
Quãng đường vật đi được từ khi ngừng tác dụng lực F là 50m.
c)
Sau 5s thì vật có vận tốc 10 m/s. Vật chịu thêm tác dụng lực F1.
Các lực tác dụng vào vật gồm :
\(\overrightarrow N ,\overrightarrow P ,\overrightarrow F ,\overrightarrow {{F_{ms}}} ,\overrightarrow {{F_1}} \)
Áp dụng định luật II Niu- tơn.
\(\overrightarrow N + \overrightarrow P + \overrightarrow F + \overrightarrow {{F_{ms}}} + \overrightarrow {{F_1}} = m.\overrightarrow a \)
Chiếu lên hai trục Ox và Oy ta có:
\(\begin{array}{l}
{\rm{Oy: N - P}} = 0 \Leftrightarrow N = P = mg\\
{\rm{Ox: F - }}{{\rm{F}}_{ms}} - {F_1} = m.{a_2} \Leftrightarrow F - \mu N - {F_1} = m{a_2}\\
= > {a_2} = \frac{{F - \mu N - {F_1}}}{m} = \frac{{F - \mu .m.g - {F_1}}}{m} = \frac{{30 - 0,1.10.10 - 45}}{{10}} = - 2,5m/{s^2}
\end{array}\)
Phương trình vận tốc là: v = v0 + a2 t = 10 – 2,5.t .
Vật dừng lại sau thời gian là: 10 – 2,5 t = 0 => t = 4s.
Vậy sau đó vật đổi chiều chuyển động.
Trong thời gian 5s sau khi tác dụng lực F1 thì vật chuyển động qua hai giai đoạn: giai đoạn chuyển động cùng chiều Ox chậm dần đều trong 4s đầu, sau đó đổi chiều chuyển động ngược với Ox với gia tốc 2,5 m/s2.
Quãng đường trong 4s đầu tiên là:
\({S_1} = \frac{{0 - {{10}^2}}}{{2.( - 2,5)}} = 20m\)
Quãng đường đi được trong 1s sau là:
\({S_2} = \frac{1}{2}.a_2^2.{t^2} = \frac{1}{2}.2,{5^2}.1 = 3,125m\)
Vậy quãng đường tổng cộng vật đi được là S = S1 + S2 = 20 + 3,125 = 23,125 (m)