Câu hỏi
Ở mặt nước, một nguồn sóng đặt tại O dao động điều hòa theo phương thẳng đứng. Sóng truyền trên mặt nước với bước sóng λ. M và N là hai điểm ở mặt nước sao cho OM = 6λ, ON = 8λ và OM vuông góc với ON. Trên đoạn thẳng MN, số điểm mà tại đó các phần tử nước dao động ngược pha với dao động của nguồn O là
- A 4
- B 5
- C 3
- D 6
Phương pháp giải:
Phương pháp : Áp dụng điều kiện để điểm H dao động ngược pha với nguồn
Lời giải chi tiết:
Đáp án A
Cách giải :
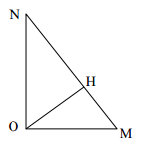
Gọi H là chân đường vuông góc hạ từ O xuongs MN
Ta có $\Delta OMN$ vuông tại O $\frac{1}{{O{H^2}}} = \frac{1}{{O{N^2}}} + \frac{1}{{O{M^2}}} = > OH = \frac{{24}}{5}\lambda $
Dể H dao động ngược pha với nguồn O thì
$\eqalign{
& {{2\pi d} \over \lambda } = \left( {2k + 1} \right)\pi = > d = \left( {2k + 1} \right){\lambda \over 2} = > \left\{ \matrix{
{{24} \over 5}\lambda \le d = \left( {2k + 1} \right){\lambda \over 2} \le 6\lambda \hfill \cr
{{24} \over 5}\lambda \le d = \left( {2k + 1} \right){\lambda \over 2} \le 8\lambda \hfill \cr} \right. \cr
& \cr} $
Giải hệ bất phương trình ta có 4 giá trị của k thỏa mãn điều kiện







