Câu hỏi
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên dưới đây
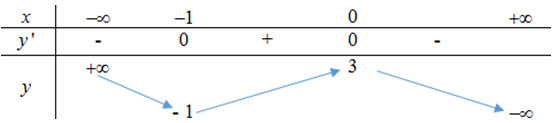
Tìm m để phương trình \(\left| {f\left( x \right)} \right| = m\) có bốn nghiệm phân biệt
- A \(0 < m < 3\).
- B \( - 1 < m < 3\).
- C \(1 < m < 3\).
- D \(m > 1\).
Phương pháp giải:
Lập bảng biến thiên của hàm số \(y = \left| {f\left( x \right)} \right|\), từ đó nhận xét số nghiệm của phương trình \(\left| {f\left( x \right)} \right| = m\).
Lời giải chi tiết:
Bảng biến thiên của hàm số \(y = \left| {f\left( x \right)} \right|\):

Số nghiệm của phương trình \(\left| {f\left( x \right)} \right| = m\) bằng số giao điểm của đồ thị hàm số và đường thẳng \(y = m\), để phương trình \(\left| {f\left( x \right)} \right| = m\) có bốn nghiệm phân biệt thì \(1 < m < 3\).
Chọn: C







