Câu hỏi
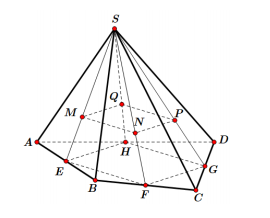
Cho khối chóp S.ABCD có thể tích bằng 81. Gọi M, N, P lần lượt là trọng tâm các mặt bên \(\left( {SAB} \right);\,\,\left( {SBC} \right);\,\,\left( {SCD} \right);\,\,\left( {SDA} \right)\). Tính thể tích V của khối chóp S.MNPQ?
- A \(V = 18\)
- B \(V = 24\)
- C \(V = 12\)
- D \(V = 54\)
Phương pháp giải:
Sử dụng công thức Simpson tính tỉ lệ thể tích, lưu ý chỉ áp dụng đối với chóp tam giác.
Lời giải chi tiết:
Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA.
Ta có \({S_{EFGH}} = \frac{1}{2}{S_{ABCD}} \Rightarrow {V_{S.EFGH}} = \frac{1}{2}{V_{S.ABCD}}\)
\(\begin{array}{l}\frac{{{V_{S.MQN}}}}{{{V_{S.EHF}}}} = \frac{{SM}}{{SE}}.\frac{{SQ}}{{SH}}.\frac{{SN}}{{SF}} = {\left( {\frac{2}{3}} \right)^2} = \frac{8}{{27}} \Rightarrow {V_{S.MQN}} = \frac{8}{{27}}{V_{S.EFH}} = \frac{8}{{27}}.\frac{1}{2}{V_{S.EFGH}} = \frac{4}{{27}}{V_{S.EFGH}}\\\frac{{{V_{S.PQN}}}}{{{V_{S.GHF}}}} = \frac{{SP}}{{SG}}.\frac{{SQ}}{{SH}}.\frac{{SN}}{{SF}} = {\left( {\frac{2}{3}} \right)^2} = \frac{8}{{27}} \Rightarrow {V_{S.PQN}} = \frac{8}{{27}}{V_{S.GHF}} = \frac{8}{{27}}.\frac{1}{2}{V_{S.EFGH}} = \frac{4}{{27}}{V_{S.EFGH}}\end{array}\)
\( \Rightarrow {V_{S.MQN}} + {V_{S.PQN}} = 2.\frac{4}{{27}}{V_{S.EFGH}} = \frac{8}{{27}}{V_{S.EFGH}} = \frac{4}{{27}} = \frac{4}{{27}}{V_{S.ABCD}} = 12\)
Chọn C.