Câu hỏi
Cho một tấm nhôm hình chữ nhật ABCD có \(AD = 24cm\). Ta gấp tấm nhôm theo hai cạnh MN, QP vào phía trong đến khi AB, CD trùng nhau như hình vẽ dưới đây để được một hình lăng trụ khuyết hai đáy. Tìm x để thể tích khối lăng trụ lớn nhất?
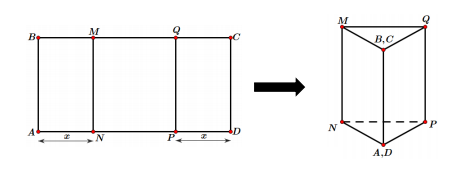
- A \(x = 8\)
- B \(x = 10\)
- C \(x = 9\)
- D \(x = 6\)
Phương pháp giải:
\(V = {S_{\Delta ANP}}.MN\), V max \( \Leftrightarrow {S_{\Delta ANP}}\) max, sử dụng BĐT Cô-si.
Lời giải chi tiết:
Đáy là tam giác cân có cạnh bên là x (cm) và cạnh đáy là \(24 - 2x\,\,\left( {cm} \right)\,\,\left( {x < 12} \right)\).
Gọi H là trung điểm của NP \( \Rightarrow AH \bot NP\).
Xét tam giác vuông ANH có: \(AH = \sqrt {A{N^2} - N{H^2}} = \sqrt {{x^2} - {{\left( {12 - x} \right)}^2}} = \sqrt {24x - 144} \) (ĐK: \(24x - 144 \ge 0 \Leftrightarrow x \ge 6\)).
\( \Rightarrow {S_{\Delta ANP}} = \frac{1}{2}AH.NP = \frac{1}{2}\sqrt {24x - 144} .\left( {24 - 2x} \right) = S\)
\( \Rightarrow V = {S_{ANP}}.AB;\,\,{V_{\max }} \Leftrightarrow {S_{ANP\,\,\max }}\) (Do AB không đổi).
Ta có:
\(\begin{array}{l}{S^2} = \frac{1}{4}{\left( {24 - 2x} \right)^2}\left( {24x - 144} \right) = \frac{1}{{{{4.6}^2}}}{\left( {144 - 12x} \right)^2}\left( {24x - 144} \right)\\ \le \frac{1}{{{{4.6}^2}}}{\left( {\frac{{144 - 12x + 144 - 12x + 24x - 144}}{3}} \right)^2} = \sqrt {786} = 16\sqrt 3 \end{array}\)
Dấu “=” xảy ra \( \Leftrightarrow 144 - 12x = 24x - 144 \Leftrightarrow x = 8\).
Chọn A.







