Câu hỏi
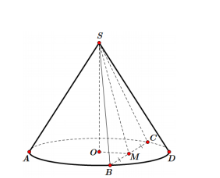
Cắt hình nón \(\left( N \right)\) có đỉnh S bởi một mặt phẳng chứa trục hình nón ta dược một tam giác vuông cân có cạnh huyền bằng \(a\sqrt 2 \); BC là một dây cung của hình tròn đáy của \(\left( N \right)\) sao cho mặt phẳng \(\left( {SBC} \right)\) tạo với đáy góc 600. Tính diện tích S của tam giác SBC.
- A \(S = \frac{{{a^2}\sqrt 2 }}{2}\)
- B \(S = \frac{{{a^2}\sqrt 3 }}{3}\)
- C \(S = \frac{{{a^2}\sqrt 2 }}{3}\)
- D \(S = \frac{{{a^2}}}{3}\)
Phương pháp giải:
+) Gọi M là trung điểm của BC, xác định góc giữa (SBC) và đáy.
+) \({S_{\Delta SBC}} = \frac{1}{2}SM.BC\).
Lời giải chi tiết:
Gọi M là trung điểm của BC \( \Rightarrow OM \bot BC\) (quan hệ vuông góc giữa đường kính và dây cung).
\( \Rightarrow BC \bot \left( {SOM} \right) \Rightarrow BC \bot SM \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {day} \right)} \right)} = \widehat {SMO} = {60^0}\)
Ta có: \(SM = \frac{{SO}}{{\sin {{60}^0}}} = \frac{{a\sqrt 6 }}{3} \Rightarrow BC = 2BM = 2\sqrt {S{B^2} - S{M^2}} = \frac{{2a}}{{\sqrt 3 }}\)
Vậy \({S_{\Delta SBC}} = \frac{1}{2}SM.BC = \frac{1}{2}.\frac{{a\sqrt 6 }}{3}.\frac{{2a}}{{\sqrt 3 }} = \frac{{{a^2}\sqrt 2 }}{3}\).
Chọn C.