Câu hỏi
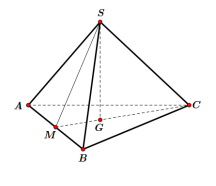
Cho hình chóp đều S.ABC có cạnh đáy bằng a, góc giữa mặt bên và đáy bằng 600. Tính diện tích xung quanh \({S_{xq}}\) của hình nón đỉnh S và có đường tròn đáy là đường tròn ngoại tiếp tam giác đáy ABC.
- A \({S_{xq}} = \frac{{\pi {a^2}\sqrt {10} }}{8}\)
- B \({S_{xq}} = \frac{{\pi {a^2}\sqrt 7 }}{6}\)
- C \({S_{xq}} = \frac{{\pi {a^2}\sqrt 3 }}{3}\)
- D \({S_{xq}} = \frac{{\pi {a^2}\sqrt 7 }}{4}\)
Phương pháp giải:
+) Xác định góc giữa mặt bên và đáy.
+) Tính chiều cao h, bán kính đáy R và đường sinh l của hình nón.
+) Sử dụng công thức \({S_{xq}} = \pi Rl\).
Lời giải chi tiết:
Gọi M là trung điểm của AB, G là trọng tâm tam giác ABC ta có: \(SG \bot \left( {ABC} \right)\) và \(\widehat {\left( {\left( {SAB} \right);\left( {ABC} \right)} \right)} = \widehat {SMG} = {60^0}\).
Ta có:
\(MG = \frac{1}{3}CM = \frac{1}{3}\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{6} \Rightarrow SG = MG.\tan {60^0} = \frac{{a\sqrt 3 }}{6}.\sqrt 3 = \frac{a}{2} = h\)
\(CG = \frac{2}{3}CM = \frac{2}{3}\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3} = R \Rightarrow l = \sqrt {{h^2} + {R^2}} = \frac{{a\sqrt {21} }}{6}\)
Vậy \({S_{xq}} = \pi Rl = \pi .\frac{{a\sqrt 3 }}{3}.\frac{{a\sqrt {21} }}{6} = \frac{{\pi {a^2}\sqrt 7 }}{6}\).
Chọn B.