Phương pháp giải:

\(d\left( {A;\left( {SBC} \right)} \right) = \frac{{3{V_{S.ABC}}}}{{{S_{SBC}}}}\).

Lời giải chi tiết:

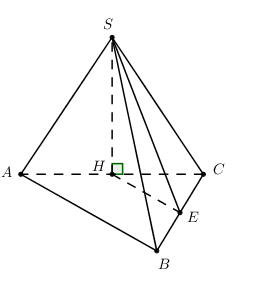
Gọi H là trung điểm của AC \( \Rightarrow SH \bot AC \Rightarrow SH \bot \left( {ABC} \right)\).

Áp dụng định lí Pytago trong tam giác vuong ABC có : \(AC = \sqrt {A{B^2} + B{C^2}}  = 2a\).

\( \Rightarrow \Delta SAC\) đều cạnh \(2a \Rightarrow SH = \frac{{2a\sqrt 3 }}{2} = a\sqrt 3 \).

\( \Rightarrow {V_{S.ABC}} = \frac{1}{3}SH.{S_{ABC}} = \frac{1}{3}.a\sqrt 3 .\frac{1}{2}.a\sqrt 3 .a = \frac{{{a^3}}}{2}\).

Gọi E là trung điểm của BC ta có HE là đường trung bình của tam giác ABC \( \Rightarrow HE//AB\) và \(HE = \frac{1}{2}AB = \frac{{a\sqrt 3 }}{2}\).

Mà \(AB \bot BC \Rightarrow HE \bot BC\). Ta có: \(\left\{ \begin{array}{l}BC \bot HE\\BC \bot SH\end{array} \right. \Rightarrow BC \bot \left( {SHE} \right) \Rightarrow BC \bot SE\).

Xét tam giác vuông SHE có: \(SE = \sqrt {S{H^2} + H{E^2}}  = \sqrt {3{a^2} + \frac{{3{a^2}}}{4}}  = \frac{{a\sqrt {15} }}{2}\).

\( \Rightarrow {S_{SBC}} = \frac{1}{2}SE.BC = \frac{1}{2}.\frac{{a\sqrt {15} }}{2}.a = \frac{{{a^2}\sqrt {15} }}{4}\).

Vậy \(d\left( {A;\left( {SBC} \right)} \right) = \frac{{3{V_{S.ABC}}}}{{{S_{SBC}}}} = \frac{{3.\frac{{{a^3}}}{2}}}{{\frac{{{a^2}\sqrt {15} }}{4}}} = \frac{{2a\sqrt {15} }}{5}\).

Chọn D.