Câu hỏi
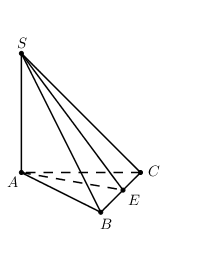
Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt đáy. \(BC = 9m,\,\,AB = 10m;\,\,AC = 17m\). Biết thể tích khối chóp S.ABC bằng \(73{m^3}\). Tính khoảng cách h từ điểm A đến mặt phẳng (SBC) ?
- A \(h = \frac{{42}}{5}m\)
- B \(h = \frac{{18}}{5}m\)
- C \(h = \sqrt {34} m\)
- D \(h = \frac{{24}}{5}m\)
Phương pháp giải:
\(d\left( {A;\left( {SBC} \right)} \right) = \frac{{3{V_{S.ABC}}}}{{{S_{SBC}}}}\).
Lời giải chi tiết:
Nửa chu vi tam giác ABC là \(p = \frac{{9 + 10 + 17}}{2} = 18\,\,\left( m \right)\)
\( \Rightarrow {S_{ABC}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = 36\,\,\left( {{m^2}} \right)\).
Kẻ \(AE \bot BC\,\,\left( {E \in BC} \right) \Rightarrow {S_{ABC}} = \frac{1}{2}AE.BC \Rightarrow AE = \frac{{2{S_{ABC}}}}{{BC}} = \frac{{2.36}}{9} = 8\,\,\left( m \right)\).
Ta có : \({V_{S.ABC}} = \frac{1}{3}SA.{S_{ABC}} \Rightarrow SA = \frac{{3{V_{SABC}}}}{{{S_{ABC}}}} = \frac{{3.73}}{{36}} = \frac{{73}}{{12}}\,\,\left( {{m^2}} \right)\)
Xét tam giác vuông SAE có : \(SE = \sqrt {S{A^2} + A{E^2}} = \frac{{\sqrt {14545} }}{{12}}\)
Ta có : \(\left\{ \begin{array}{l}BC \bot AE\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAE} \right) \Rightarrow BC \bot SE\)
\( \Rightarrow {S_{SBC}} = \frac{1}{2}SE.BC = \frac{1}{2}.\frac{{\sqrt {14545} }}{{12}}.9 = \frac{{3\sqrt {14545} }}{8}\).
Vậy \(d\left( {A;\left( {SBC} \right)} \right) = \frac{{3{V_{S.ABC}}}}{{{S_{SBC}}}} = \frac{{3.73}}{{\frac{{3\sqrt {14545} }}{8}}} \approx 4,84\,\,\left( m \right)\).
Chọn D.