Phương pháp giải:

Vẽ đồ thị hàm số \(y = \left| {{x^2} - 3x + 1} \right|\). Tìm điều kiện của m để đường thẳng \(y = m\) cắt \(y = \left| {{x^2} - 3x + 1} \right|\) tại 4 điểm phân biệt.

Lời giải chi tiết:

\(y = \left| {{x^2} - 3x + 1} \right| = \left[ \begin{array}{l}{x^2} - 3x + 1\,\,khi\,\,x \in \left( { - \infty ;\frac{{3 - \sqrt 5 }}{2}} \right) \cup \left( {\frac{{3 + \sqrt 5 }}{2}; + \infty } \right)\\ - {x^2} + 3x - 1\,\,khi\,\,x \in \left( {\frac{{3 - \sqrt 5 }}{2};\frac{{3 + \sqrt 5 }}{2}} \right)\end{array} \right.\)

Vẽ hai đồ thị hàm số trên cùng 1 mặt phẳng tọa độ :

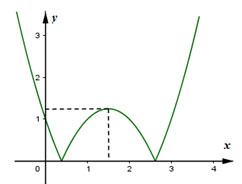
Hàm số \(y =  - {x^2} + 3x - 1\) có tọa độ đỉnh \(I\left( {\frac{3}{2};\frac{5}{4}} \right)\)

Để đồ thị hàm số \(y = \left| {{x^2} - 3x + 1} \right|\) cắt đường thẳng \(y = m\) tại 4 điểm phân biệt \( \Leftrightarrow 0 < m < \frac{5}{4}\).

Chọn B.