Câu hỏi
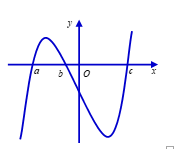
Cho hàm số \(y = f\left( x \right)\) có đạo hàm là hàm số liên tục trên R với đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ.
Biết \(f\left( a \right) > 0\), hỏi đồ thị hàm số \(y = f\left( x \right)\) cắt trục hoành tại nhiều nhất bao nhiêu điểm?
- A 3
- B 2
- C 4
- D 0
Phương pháp giải:
Từ đồ thị hàm số \(y = f'\left( x \right)\) lập BBT của đồ thị hàm số \(y = f\left( x \right)\) và kết luận.
Lời giải chi tiết:
Từ đồ thị hàm số \(y = f'\left( x \right)\), ta có bảng biến thiên:
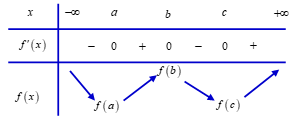
Do \(f\left( a \right) > 0\), suy ra \(y = f\left( x \right)\) có thể cắt trục hoành nhiều nhất tại \(2\) điểm.
Chọn B.
Câu hỏi trước
