Câu hỏi
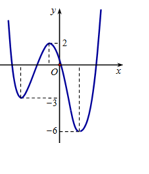
Cho đồ thị của hàm số \(y = f\left( x \right)\) như hình vẽ dưới đây:
Gọi \(S\) là tập hợp các giá trị nguyên dương của tham số \(m\) để hàm số \(y = \left| {f\left( {x - 2017} \right) + m} \right|\) có \(5\) điểm cực trị. Tổng tất cả các giá trị của các phần tử của tập \(S\) bằng
- A \(12\).
- B \(15\).
- C \(18\).
- D \(9\).
Lời giải chi tiết:
Nhận xét: Số giao điểm của \(\left( C \right):y = f\left( x \right)\) với \(Ox\) bằng số giao điểm của \(\left( {C'} \right):y = f\left( {x - 2017} \right)\) với \(Ox\).
Vì \(m > 0\) nên \(\left( {C''} \right):y = f\left( {x - 2017} \right) + m\) có được bằng cách tịnh tiến \(\left( {C'} \right):y = f\left( {x - 2017} \right)\) lên trên \(m\) đơn vị.
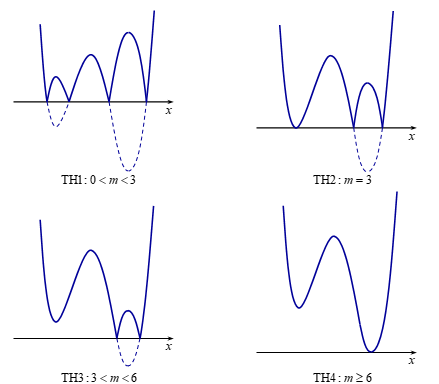
TH1: \(0 < m < 3\). Đồ thị hàm số có \(7\) điểm cực trị. Loại.
TH2: \(m = 3\). Đồ thị hàm số có \(5\) điểm cực trị. Nhận.
TH3: \(3 < m < 6\). Đồ thị hàm số có \(5\) điểm cực trị. Nhận.
TH4: \(m \ge 6\). Đồ thị hàm số có \(3\) điểm cực trị. Loại.
Vậy \(3 \le m < 6\). Do \(m \in {Z^*}\) nên \(m \in \left\{ {3;4;5} \right\}\).
Vậy tổng giá trị tất cả các phần tử của \(S\) bằng \(12\).
Chọn A.