Câu hỏi
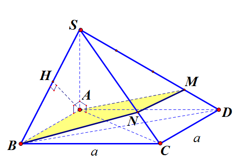
Cho khối chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), \(SA\) vuông góc với mặt phẳng đáy và khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng \(\frac{{a\sqrt 2 }}{2}\). Gọi \(M\) là điểm thuộc cạnh \(SD\) sao cho \(\overrightarrow {SM} = 3\overrightarrow {MD} \). Mặt phẳng \(\left( {ABM} \right)\) cắt cạnh \(SC\) tại điểm \(N\). Thể tích khối đa diện \(MNABCD\) bằng
- A \(\frac{{7{a^3}}}{{32}}\).
- B \(\frac{{15{a^3}}}{{32}}\).
- C \(\frac{{17{a^3}}}{{32}}\).
- D \(\frac{{11{a^3}}}{{96}}\).
Phương pháp giải:
+) Xác định điểm N.
+) Phân chia và lắp ghép các khối đa diện.
Lời giải chi tiết:
Kẻ \(AH \bot SB\) \( \Rightarrow d\left( {A,\,\left( {SBC} \right)} \right) = AH = \frac{{a\sqrt 2 }}{2}\) \( \Rightarrow \Delta SAB\) vuông cân tại \(A\) \( \Rightarrow SA = a\).
\( \Rightarrow {V_{S.ABCD}} = \frac{1}{3}SA.{S_{ABCD}} = \frac{1}{3}.a.{a^2} = \frac{{{a^3}}}{3}\).
Kẻ \(MN{\rm{//}}CD \Rightarrow \frac{{SM}}{{SD}} = \frac{{SN}}{{SC}} = \frac{3}{4}\).
Ta có: \({V_{S.ABD}} = {V_{S.BCD}} = \frac{1}{2}{V_{S.ABCD}}\)
\(\frac{{{V_{S.AMNB}}}}{{{V_{S.ABCD}}}} = \frac{{{V_{S.ABM}} + {V_{S.BMN}}}}{{2{V_{S.ABD}}}} = \frac{1}{2}\left( {\frac{{{V_{S.ABM}}}}{{{V_{S.ABD}}}} + \frac{{{V_{S.BMN}}}}{{{V_{S.BCD}}}}} \right) = \frac{1}{2}\left( {\frac{{SM}}{{SD}} + \frac{{SM}}{{SD}}.\frac{{SN}}{{SC}}} \right) = \frac{1}{2}\left( {\frac{3}{4} + \frac{3}{4}.\frac{3}{4}} \right) = \frac{{21}}{{32}}\).
\( \Rightarrow \frac{{{V_{MNABCD}}}}{{{V_{S.ABCD}}}} = \frac{{{V_{S.ABCD}} - {V_{S.AMNB}}}}{{{V_{S.ABCD}}}} = 1 - \frac{{{V_{S.AMNB}}}}{{{V_{S.ABCD}}}} = 1 - \frac{{21}}{{32}} = \frac{{11}}{{32}}\).
Vậy \({V_{MNABCD}} = \frac{{11}}{{32}}{V_{S.ABCD}} = \frac{{11}}{{32}}.\frac{{{a^3}}}{3} = \frac{{11{a^3}}}{{96}}\).
Chọn D.