Câu hỏi
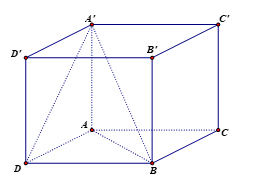
Gọi \({V_1}\) là thể tích của khối lập phương \(ABCD.A'B'C'D'\), \({V_2}\) là thể tích khối tứ diện \(A'ABD\). Hệ thức nào sau đây là đúng?
- A \({V_1} = 4{V_2}\).
- B \({V_1} = 6{V_2}\).
- C \({V_1} = 2{V_2}\).
- D \({V_1} = 8{V_2}\).
Phương pháp giải:
So sánh chiều cao và diện tích đáy của khối chóp so với hình lập phương.
Lời giải chi tiết:
Gọi \(a\) là độ dài cạnh hình lập phương. Thể tích khối lập phương: \({V_1} = {a^3}\).
Thể tích khối tứ diện \(ABDA'\):
\({V_2} = \frac{1}{3}.AA'.{S_{ABD}} = \frac{1}{3}.a.\frac{{{a^2}}}{2} = \frac{{{a^3}}}{6}\).
Vậy \({V_1} = 6{V_2}\).
Chọn B.
Câu hỏi trước
