Phương pháp giải:

Thể tích khối chóp: \(V = \frac{1}{3}Sh\).

Lời giải chi tiết:

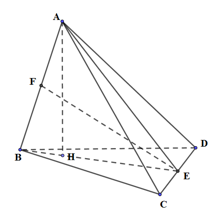
Gọi E, F lần lượt là trung điểm của CD, AB. Kẻ AH vuông góc với BE tại H.

Theo đề bài ta có: AB = CD = a, BC = BD = AC = AD = b

\( \Rightarrow \)\(AE = BE = \sqrt {{b^2} - \frac{{{a^2}}}{4}} \)

Ta có: \({S_{\Delta BCD}} = \frac{1}{2}BE.CD = \frac{1}{2}.\sqrt {{b^2} - \frac{{{a^2}}}{4}} .a\)

\(EF = \sqrt {B{E^2} - B{F^2}}  = \sqrt {{b^2} - \frac{{{a^2}}}{4} - \frac{{{a^2}}}{4}}  = \sqrt {{b^2} - \frac{{{a^2}}}{2}} \)

\({S_{\Delta ABE}} = \frac{1}{2}AH.BE = \frac{1}{2}\,EF.AB \Rightarrow AH.BE = EF.AB \Leftrightarrow AH.\sqrt {{b^2} - \frac{{{a^2}}}{4}}  = \sqrt {{b^2} - \frac{{{a^2}}}{2}} .a \Leftrightarrow AH = \frac{{\sqrt {{b^2} - \frac{{{a^2}}}{2}} .a}}{{\sqrt {{b^2} - \frac{{{a^2}}}{4}} }}\)

Thể tích khối tứ diện ABCD:  \(V = \frac{1}{3}AH.{S_{\Delta BCD}} = \frac{1}{3}.\frac{{\sqrt {{b^2} - \frac{{{a^2}}}{2}} .a}}{{\sqrt {{b^2} - \frac{{{a^2}}}{4}} }}.\frac{1}{2}.\sqrt {{b^2} - \frac{{{a^2}}}{4}} .a = \frac{{{a^2}\sqrt {{b^2} - \frac{{{a^2}}}{2}} }}{6}\).

Chọn: B