Câu hỏi
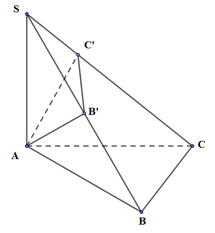
Cho hình chóp S.ABC có \(SA \bot (ABC)\), tam giác ABC vuông tại B. Biết \(SA = a\), \(AB = b,\;BC = c\). Gọi B’, C’ tương ứng là hình chiếu vuông góc của A trên SB, SC. Gọi V, V’ tương ứng là thể tích của các khối chóp S.ABC, S.AB’C’. Khi đó ta có
- A \(\frac{{V'}}{V} = \frac{{{a^2}}}{{{a^2} + {b^2}}}\).
- B \(\frac{{V'}}{V} = \frac{{{a^2}}}{{{a^2} + {b^2} + {c^2}}}\).
- C \(\frac{{V'}}{V} = \frac{{{a^4}}}{{\left( {{a^2} + {b^2}} \right)\left( {{a^2} + {b^2} + {c^2}} \right)}}\).
- D \(\frac{{V'}}{V} = \frac{{{a^2}}}{{{a^2} + {b^2}}} + \frac{{{a^2}}}{{{a^2} + {b^2} + {c^2}}}\).
Phương pháp giải:
Sử dụng công thức tỉ số thể tích cho khối chóp tam giác (Công thức Simson):
Cho khối chóp S.ABC, các điểm \({A_1},\,{B_1},\,{C_1}\) lần lượt thuộc \(SA,\,SB,\,SC\). Khi đó,
\(\frac{{{V_{S.\,{A_1}{B_1}{C_1}}}}}{{{V_{S.ABC}}}} = \frac{{S{A_1}}}{{SA}}.\frac{{S{B_1}}}{{SB}}.\frac{{S{C_1}}}{{SC}}\)
Lời giải chi tiết:
Tam giác SAB vuông tại A, AB’ vuông góc SB
\( \Rightarrow SB'.SB = S{A^2} \Rightarrow \frac{{SB'}}{{SB}} = \frac{{S{A^2}}}{{S{B^2}}} = \frac{{{a^2}}}{{{a^2} + {b^2}}}\)
Tam giác ABC vuông tại B
\( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {b^2}} \)
Tam giác SAC vuông tại A, AC’ vuông góc SC
\(\begin{array}{l} \Rightarrow SC'.SC = S{A^2} \Rightarrow \frac{{SC'}}{{SC}} = \frac{{S{A^2}}}{{S{C^2}}} = \frac{{{a^2}}}{{{a^2} + {b^2} + {c^2}}}\\\frac{{{V_{S.\,AB'C'}}}}{{{V_{S.ABC}}}} = \frac{{SB'}}{{SB}}.\frac{{SC'}}{{SC}} = \frac{{{a^2}}}{{{a^2} + {b^2}}}.\frac{{{a^2}}}{{{a^2} + {b^2} + {c^2}}} = \frac{{{a^4}}}{{\left( {{a^2} + {b^2}} \right)\left( {{a^2} + {b^2} + {c^2}} \right)}}\end{array}\)
Chọn: C