Câu hỏi
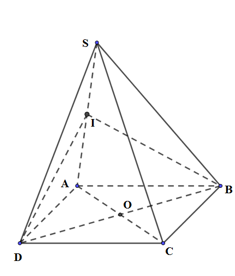
Cho hình chóp S.ABCD đáy ABCD là hình thoi. SA = x \(\left( {0 < x < \sqrt 3 } \right)\) các cạnh còn lại đều bằng 1. Thể tích của khối chóp S.ABCD là
- A \(\frac{{x\sqrt {3 - {x^2}} }}{3}.\)
- B \(\frac{{{x^2}\sqrt {3 - {x^2}} }}{6}.\)
- C \(\frac{{{x^2}.\sqrt {3 - {x^2}} }}{3}.\)
- D \(\frac{{x.\sqrt {3 - {x^2}} }}{6}.\)
Phương pháp giải:
\({V_{S.ABCD}} = 2{V_{S.ABD}}\)
Lời giải chi tiết:
ABCD là hình thoi \( \Rightarrow \Delta ABD = \Delta CBD \Rightarrow {S_{\Delta ABD}} = {S_{\Delta CBD}}\)
\( \Rightarrow {V_{S.ABCD}} = 2{V_{S.ABD}}\).
Gọi I là trung điểm của SA, O là tâm của hình thoi ABCD.
Ta có: \(\Delta SAD,\,\,\Delta SAB\) là hai tam giác cân lần lượt tại D và B
\( \Rightarrow DI \bot SA,\,\,BI \bot SA \Rightarrow SA \bot \left( {IBD} \right)\)
\({V_{S.ABD}} = {V_{S.IBD}} + {V_{I.ABD}} = \frac{1}{3}.SI.{S_{\Delta IBD}} + \frac{1}{3}.IA.{S_{\Delta IBD}} = \frac{1}{3}.SA.{S_{\Delta IBD}}\)
Tam giác IAD vuông tại I \( \Rightarrow DI = \sqrt {A{D^2} - I{A^2}} = \sqrt {1 - \frac{{{x^2}}}{4}} \)
\( \Rightarrow IB = ID = \sqrt {1 - \frac{{{x^2}}}{4}} \)
IO là đường trung bình của tam giác SAC \( \Rightarrow IO = \frac{{SC}}{2} = \frac{1}{2}\)
Tam giác IBD cân tại I, O là trung điểm của BD \( \Rightarrow IO \bot BD\) \( \Rightarrow \Delta IOD\) vuông tại O
\( \Rightarrow OD = \sqrt {I{D^2} - I{O^2}} = \sqrt {1 - \frac{{{x^2}}}{4} - \frac{1}{4}} = \sqrt {\frac{3}{4} - \frac{{{x^2}}}{4}} \Rightarrow BD = \sqrt {3 - {x^2}} \)
Diện tích tam giác IBD: \({S_{IBD}} = \frac{1}{2}.IO.BD = \frac{1}{2}.\frac{1}{2}.\sqrt {3 - {x^2}} = \frac{{\sqrt {3 - {x^2}} }}{4}\)
\( \Rightarrow {V_{S.ABD}} = \frac{1}{3}.SA.{S_{\Delta IBD}} = \frac{1}{3}.x.\frac{{\sqrt {3 - {x^2}} }}{4} = \frac{{x\sqrt {3 - {x^2}} }}{{12}} \Rightarrow {V_{S.ABCD}} = 2{V_{S.ABD}} = \frac{{x\sqrt {3 - {x^2}} }}{6}\).
Chọn: D