Câu hỏi
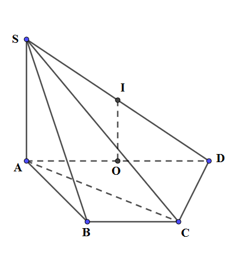
Cho hình chóp \(S.ABCD\) có đường cao \(SA = 4a\) ; \(ABCD\) là hình thang với đáy lớn AD, biết\(AD = 4a,AB = BC = CD = 2a\). Thể tích của khối cầu ngoại tiếp hình chóp \(S.ABC\) bằng
- A \(64\pi {a^3}\sqrt 2 .\)
- B \(\frac{{64\pi {a^3}\sqrt 2 }}{3}.\)
- C \(\frac{{32\pi {a^3}\sqrt 2 }}{3}.\)
- D \(32\pi {a^3}\sqrt 2 .\)
Phương pháp giải:
Xác định trục của hai mặt phẳng bất kì của chóp (Thường là mặt đáy và một mặt bên). Giao điểm của chúng chính là tâm mặt cầu ngoại tiếp khối chóp.
Lời giải chi tiết:
Gọi O, I lần lượt là trung điểm của AD và SD
Dễ dàng chứng minh: ABCD là hình thang cân (\(AD = 4a,AB = BC = CD = 2a\)) và O là tâm đường tròn ngoại tiếp ABCD.
IO là đường trung bình của tam giác SAC \( \Rightarrow IO//SA\)
Mà \(SA \bot \left( {ABCD} \right) \Rightarrow IO \bot \left( {ABCD} \right) \Rightarrow IA = IB = IC\) (1)
Tam giác SAD vuông tại A \( \Rightarrow IA = IS = \frac{{SD}}{2} = \frac{{4a\sqrt 2 }}{2} = 2a\sqrt 2 \) (2)
Từ (1) và (2) suy ra I là tâm mặt cầu ngoại tiếp tứ diện SABC và bán kính mặt cầu \(R = 2a\sqrt 2 \)
Thể tích của khối cầu ngoại tiếp hình chóp \(S.ABC\) bằng \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi .{\left( {2a\sqrt 2 } \right)^3} = \frac{{64\sqrt 2 \pi {a^3}}}{3}\).
Chọn: B