Câu hỏi
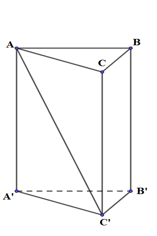
Cho lăng trụ đứng tam giác ABC.A’B’C’, đáy là tam giác vuông tại A, \(AC = a,\;\,\widehat {ACB} = {60^o},\;\,AC' = 3a.\) Thể tích khối lăng trụ đó là
- A \(\frac{{4{a^3}.\sqrt 6 }}{3}\).
- B \(\sqrt 6 .{a^3}\) .
- C \(\frac{{2{a^3}.\sqrt 6 }}{3}\).
- D \(\frac{{{a^3}.\sqrt 6 }}{3}\).
Phương pháp giải:
Thể tích khối lăng trụ: \(V = Sh\).
Lời giải chi tiết:
Tam giác ABC vuông tại A \( \Rightarrow AB = AC.\tan \widehat {ACB} = a.\tan 60^\circ = a\sqrt 3 \)
Diện tích tam giác ABC: \(S = \frac{1}{2}AB.AC = \frac{1}{2}.a\sqrt 3 .a = \frac{{{a^2}\sqrt 3 }}{2}\)
Tam giác AA’C’ vuông tại A’ \( \Rightarrow AA' = \sqrt {AC{'^2} - A'C{'^2}} = \sqrt {{{\left( {3a} \right)}^2} - {a^2}} = 2\sqrt 2 a\)
Thể tích khối lăng trụ đó là: \(V = Sh = \frac{{{a^2}\sqrt 3 }}{2}.2\sqrt 2 a = {a^3}\sqrt 6 \).
Chọn: B
Câu hỏi trước
