Câu hỏi
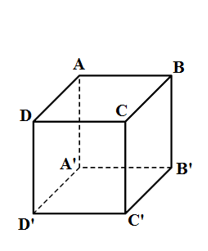
Khối lập phương ABCD.A’B’C’D’ có độ dài đoạn \(AB' = 2a\). Thể tích của khối đó là
- A \(2\,\sqrt 2 \,{a^3}.\)
- B \(8\,{a^3}.\)
- C \(3\,\sqrt 3 \,{a^3}.\)
- D \(3\,\sqrt 2 \,{a^3}.\)
Phương pháp giải:
Thể tích khối lập phương có các cạnh đều bằng a là: \(V = {a^3}\).
Lời giải chi tiết:
ABB’A’ là hình vuông có AB’ = 2a
\( \Rightarrow AB = \frac{{AB'}}{{\sqrt 2 }} = \frac{{2a}}{{\sqrt 2 }} = a\sqrt 2 \)
Thể tích của khối đó là: \(V = {\left( {a\sqrt 2 } \right)^3} = 2\sqrt 2 {a^3}\).
Chọn: A
Câu hỏi trước
