Câu hỏi
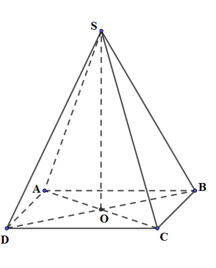
Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng \({60^0}\). Thể tích khối chóp là
- A \(\frac{{\sqrt 3 \,{a^3}}}{6}.\)
- B \(\frac{{\sqrt 6 \,{a^3}}}{3}.\)
- C \(\frac{{\sqrt 6 \,{a^3}}}{6}.\)
- D \(\frac{{\sqrt 2 \,{a^3}}}{6}.\)
Phương pháp giải:
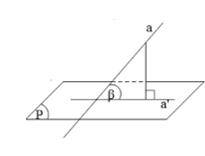
* Xác định góc giữa đường thẳng và mặt phẳng:
- Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P).
- Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.
Lời giải chi tiết:
Ta có: \(SO \bot \left( {ABCD} \right) \Rightarrow \left( {\widehat {SA;\left( {ABCD} \right)}} \right) = \left( {\widehat {SA;AO}} \right) = \widehat {SAO} = 60^\circ \)
\(ABCD\) là hình vuông cạnh a \( \Rightarrow \left\{ \begin{array}{l}{S_{ABCD}} = {a^2}\\AC = a\sqrt 2 \Rightarrow OA = \frac{{AC}}{2} = \frac{a}{{\sqrt 2 }}\end{array} \right.\)
\(\Delta SOA\) vuông tại O \( \Rightarrow SO = OA.\tan \widehat {SAO} = \frac{a}{{\sqrt 2 }}.\tan 60^\circ = \frac{{a\sqrt 3 }}{{\sqrt 2 }}\)
Thể tích của khối chóp là: \(V = \frac{1}{3}.SO.{S_{ABCD}} = \frac{1}{3}.\frac{{a\sqrt 3 }}{{\sqrt 2 }}.{a^2} = \frac{{\sqrt 6 {a^3}}}{6}\).
Chọn: C