Câu hỏi
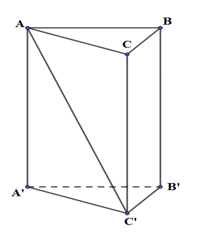
Hình lăng trụ đứng ABC.A’B’C’, đáy là tam giác ABC vuông tại A, có AB = a, BC = 2a, góc giữa AC’ và mặt phẳng đáy bằng \({60^0}\). Hình trụ ngoại tiếp hình lăng trụ ABC.A’B’C’ có diện tích toàn phần là
- A \(3\sqrt 3 \,\pi {a^2}.\)
- B \(6\pi {a^2}.\)
- C \(7\pi {a^2}.\)
- D \(8\pi {a^2}\).
Phương pháp giải:
Diện tích xung quanh của hình trụ: \({S_{xq}} = 2\pi Rh\)
Diện tích toàn phần của hình trụ: \({S_{tp}} = {S_{xq}} + {S_{2\,day}} = 2\pi Rh + 2\pi {R^2}\)
Lời giải chi tiết:
Ta có: ABC.A’B’C’ là lăng trụ đứng \( \Rightarrow AA' \bot \left( {A'B'C'} \right)\)
\( \Rightarrow \left( {\widehat {AC';\left( {A'B'C'} \right)}} \right) = \left( {\widehat {AC';A'C'}} \right) = \widehat {AC'A'} = 60^\circ \)
Tam giác ABC vuông tại A \( \Rightarrow AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{\left( {2a} \right)}^2} - {a^2}} = a\sqrt 3 \)
Tam giác AA’C’ vuông tại A’
\( \Rightarrow AA\,' = A'C'.\tan 60^\circ = AC.\tan 60^\circ = a\sqrt 3 .\sqrt 3 = 3a\)
Hình trụ ngoại tiếp hình lăng trụ ABC.A’B’C’ có đường cao \(h = AA' = 3a\), bán kính đáy \(R = \frac{{BC}}{2} = \frac{{2a}}{2} = a\)
Diện tích toàn phần của hình trụ là: \({S_{tp}} = 2\pi Rh + 2\pi {R^2} = 2\pi .a.3a + 2\pi {a^2} = 8\pi {a^2}\).
Chọn: D