Câu hỏi
Cho \(f(x) = - {x^2} + 3x - 2;f(x) \ge 0\). Nghiệm của bất phương trình là?
- A \(\left[ {1;2} \right]\)
- B \(\left( { - \infty ;1} \right) \cup \left( {2; + \infty } \right)\)
- C \(\left( { - \infty ; - 1} \right) \cup \left( {2; + \infty } \right)\)
- D \(\left( { - \infty ;1} \right] \cup \left[ {2; + \infty } \right)\)
Phương pháp giải:
Sử dụng quy tắc trong trái ngoài cùng.
Lời giải chi tiết:
Với \(f(x) = - {x^2} + 3x - 2;\)ta có: \(a = 1;\,\,\Delta = 1;\,\,f\left( x \right) = 0\) có hai nghiệm \({x_1} = 1;\,\,{x_2} = 2\).
Bảng xét dấu
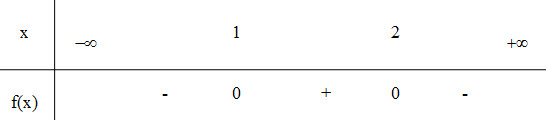
Chọn A.
Câu hỏi trước
