Câu hỏi
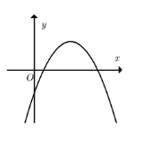
Cho hàm số \(y = a{x^2} + bx + c\) có đồ thị như hình bên. Khẳng định nào sau đây đúng?
- A \(a < 0;\,\,b > 0;\,\,c > 0\).
- B \(a > 0;\,\,b < 0;\,\,c > 0\)
- C \(a < 0\,\,;b > 0;\,\,c < 0\)
- D \(a > 0;\,\,b > 0;\,\,c < 0\)
Phương pháp giải:
Dựa vào bề lõm của đồ thị hàm số \( \Rightarrow \) dấu của a.
Dựa vào hoành độ đỉnh và dấu của a suy ra dấu của b.
Dựa vào giao điểm của đồ thị hàm số với trục tung suy ra dấu của c.
Lời giải chi tiết:
Đồ thị hàm số có bề lõm hướng xuống \( \Rightarrow a < 0\).
Hoành độ đỉnh \(x = \frac{{ - b}}{{2a}} > 0\), mà \(a < 0 \Rightarrow b > 0\).
Parabol cắt trục tung tại điểm \(\left( {0;c} \right)\) nằm phía dưới trục hoành \( \Rightarrow c < 0\).
Chọn C.