Câu hỏi
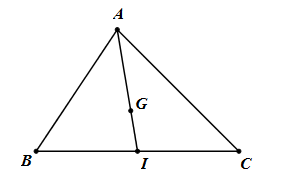
Cho tam giác ABC có G là trọng tâm, I là trung điểm của BC. Tìm khẳng định sai?
- A \(\left| {\overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {IA} } \right| = IA\)
- B \(\left| {\overrightarrow {IB} + \overrightarrow {IC} } \right| = \overrightarrow {BC} \)
- C \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = 2AI\)
- D \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = 3GA\)
Phương pháp giải:
I là trung điểm của BC \( \Rightarrow \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \).
Lời giải chi tiết:
Do I là trung điểm của BC \( \Rightarrow \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \Rightarrow \left| {\overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {IA} } \right| = \left| {\overrightarrow {IA} } \right| = IA \Rightarrow A\) đúng.
\(\overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \Rightarrow \left| {\overrightarrow {IB} + \overrightarrow {IC} } \right| = 0 \Rightarrow B\) sai.
Chọn đáp án B.