Câu hỏi
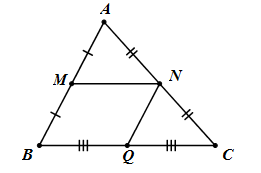
Cho hình bình hành ABCD có M, Q, N là trung điểm của AB, BC, CA. Khi đó vectơ \(\overrightarrow {AB} + \overrightarrow {BM} + \overrightarrow {NA} + \overrightarrow {BQ} \) là vectơ nào sau đây?
- A \(\overrightarrow 0 \)
- B \(\overrightarrow {BC} \)
- C \(\overrightarrow {AQ} \)
- D \(\overrightarrow {CB} \)
Phương pháp giải:
+) Sử dụng công thức ba điểm đơn giản biểu thức \(\overrightarrow {AB} + \overrightarrow {BM} + \overrightarrow {NA} + \overrightarrow {BQ} \).
+) Sử dụng tính chất đường trung bình của tam giác.
Lời giải chi tiết:
\(\begin{array}{l}\,\,\,\,\overrightarrow {AB} + \overrightarrow {BM} + \overrightarrow {NA} + \overrightarrow {BQ} \\ = \overrightarrow {AM} + \overrightarrow {NA} + \overrightarrow {BQ} \\ = \overrightarrow {NA} + \overrightarrow {AM} + \overrightarrow {BQ} \\ = \overrightarrow {NM} + \overrightarrow {BQ} \end{array}\)
Ta có MN là đường trung bình của tam giác ABC \( \Rightarrow MN = \frac{{BC}}{2} = BQ \Rightarrow \overrightarrow {NM} = - \overrightarrow {BQ} \Rightarrow \overrightarrow {NM} + \overrightarrow {BQ} = \overrightarrow 0 \)
Chọn đáp án A.