Câu hỏi
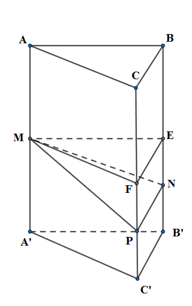
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có thể tích bằng \(V\). Các điểm \(M,\,N,\,P\) lần lượt thuộc cạnh \(AA',\,BB',\,CC'\) sao cho \(\frac{{AM}}{{AA'\,}} = \frac{1}{2},\,\,\frac{{BN}}{{BB'}} = \frac{{CP}}{{CC'}} = \frac{3}{4}\). Thể tích khối đa diện \(ABC.MNP\) là:
- A \(\frac{2}{3}V\).
- B \(\frac{1}{8}V\).
- C \(\frac{1}{3}V\).
- D \(\frac{1}{2}V\).
Phương pháp giải:
Phân chia và lắp ghép các khối đa diện.
Lời giải chi tiết:
Gọi E, F lần lượt là trung điểm của BB’, CC’. Khi đó: ABC.MEF là hình lăng trụ đứng và \({V_{ABC.MEF}} = \frac{1}{2}V\)
Ta có:
\({V_{M.EFNP}} = \frac{1}{4}{V_{M.BCC'B'}} = \frac{1}{4}.{V_{A.BCC'B'}} = \frac{1}{4}.\left( {V - {V_{A.A'B'C'}}} \right) = \frac{1}{4}\left( {V - \frac{V}{3}} \right) = \frac{1}{4}.\frac{2}{3}V = \frac{V}{6}\)
\( \Rightarrow {V_{ABC.MNP}} = {V_{ABC.MEF}} + {V_{M.EFNP}} = \frac{1}{2}V + \frac{1}{6}V = \frac{2}{3}V\).
Chọn: A
Câu hỏi trước
