Câu hỏi
Tìm các giá trị thực của tham số m sao cho phương trình \({x^3} - 3x + 4m - 1 = 0\) có ít nhất một nghiệm thực trong đoạn \(\left[ { - 3;4} \right]\)?
- A \(\frac{{ - 51}}{4} \le m \le \frac{{19}}{4}\).
- B \(\frac{{ - 51}}{4} < m < \frac{{19}}{4}\).
- C \( - 51 < m < 19\).
- D \( - 51 \le m \le 19\).
Phương pháp giải:
Tìm miền giá trị của hàm số \(y = {x^3} - 3x - 1\) trên đoạn \(\left[ { - 3;4} \right]\)
Từ đó, xác định giá trị của m để phương trình đã cho có nghiệm trên đoạn \(\left[ { - 3;4} \right]\).
Lời giải chi tiết:
\({x^3} - 3x + 4m - 1 = 0 \Leftrightarrow {x^3} - 3x - 1 = - 4m\) (*)
Xét hàm số \(y = {x^3} - 3x - 1\) trên đoạn \(\left[ { - 3;4} \right]\)
Ta có: \(y' = 3{x^2} - 3,\,\,y' = 0 \Leftrightarrow x = \pm 1\)
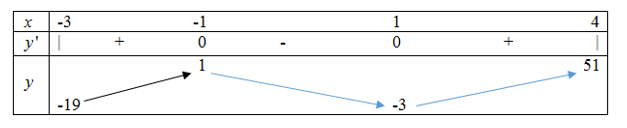
Bảng biến thiên:
Để phương trình (*) có nghiệm thì \( - 19 \le - 4m \le 51 \Leftrightarrow - \frac{{51}}{4} \le m \le \frac{{19}}{4}\).
Chọn: A