Câu hỏi
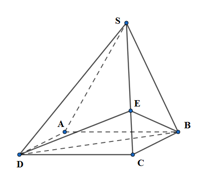
Cho hình chóp\(S.ABCD\) có đáy \(ABCD\) là hình bình hành và có thể tích bằng 1. Trên cạnh \(SC\)lấy điểm \(E\) sao cho \(SE = 2EC\). Tính thể tích \(V\) của khối tứ diện \(SEBD\).
- A \(V = \frac{1}{3}\).
- B \(V = \frac{2}{3}\).
- C \(V = \frac{1}{6}\).
- D \(V = \frac{1}{{12}}\).
Phương pháp giải:
Sử dụng công thức tỉ số thể tích cho khối chóp tam giác
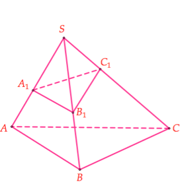
(Công thức Simson): Cho khối chóp S.ABC, các điểm \({A_1},\,{B_1},\,{C_1}\) lần lượt thuộc \(SA,\,SB,\,SC\). Khi đó, \(\frac{{{V_{S.\,{A_1}{B_1}{C_1}}}}}{{{V_{S.ABC}}}} = \frac{{S{A_1}}}{{SA}}.\frac{{S{B_1}}}{{SB}}.\frac{{S{C_1}}}{{SC}}\).
Lời giải chi tiết:
Ta có: \(\frac{{{V_{S.EBD}}}}{{{V_{S.CBD}}}} = \frac{{SE}}{{SC}} = \frac{2}{3} \Rightarrow {V_{S.EBD}} = \frac{2}{3}{V_{S.CBD}}\)
Mà \({V_{S.CBD}} = \frac{1}{2}{V_{S.ABCD}}\) (do \({S_{BCD}} = \frac{1}{2}{S_{ABCD}}\))
\( \Rightarrow {V_{S.EBD}} = \frac{2}{3}.\frac{1}{2}{V_{S.ABCD}} = \frac{1}{3}.1 = \frac{1}{3}\) .
Chọn: A