Phương pháp giải:

+) Xác định góc giữa hai mặt phẳng (A’BC) và (ABC).

+) Đặt \(AB = x\), tính diện tích tam giác A’BC theo x, từ đó tìm x.

+) \({V_{ABC.A'B'C'}} = AA'.{S_{\Delta ABC}}\).

Lời giải chi tiết:

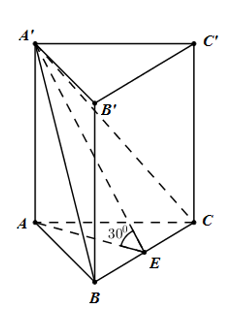
Gọi E là trung điểm của BC ta có:

\(\left\{ \begin{array}{l}AE \bot BC\\AA' \bot BC\end{array} \right. \Rightarrow BC \bot \left( {AA'E} \right) \Rightarrow BC \bot A'E\)

\( \Rightarrow \widehat {\left( {\left( {A'BC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {A'E;AE} \right)} = \widehat {A'EA} = {30^0}\)

Đặt \(AB = x\) ta có: \(AE = \frac{{x\sqrt 3 }}{2}\)

\( \Rightarrow \cos {30^0} = \frac{{AE}}{{A'E}} \Rightarrow A'E = \frac{{AE}}{{\cos {{30}^0}}} = x\)

\( \Rightarrow {S_{\Delta A'BC}} = \frac{1}{2}A'E.BC = \frac{1}{2}{x^2} = 8{a^2} \Leftrightarrow {x^2} = 16{a^2} \Leftrightarrow x = 4a\)

\( \Rightarrow {S_{\Delta ABC}} = \frac{{{{\left( {4a} \right)}^2}\sqrt 3 }}{4} = 4\sqrt 3 {a^2}\) Xét tam giác vuông A’AE có \(AA' = AE.\tan {30^0} = \frac{{4a\sqrt 3 }}{2}.\frac{{\sqrt 3 }}{3} = 2a\)

Vậy \({V_{ABC.A'B'C'}} = AA'.{S_{\Delta ABC}} = 2a.4\sqrt 3 {a^2} = 8\sqrt 3 {a^3}\).

Chọn đáp án A.