Câu hỏi
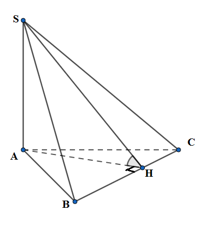
Cho khối chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\); tam giác \(ABC\) vuông tại \(A\), biết \(BC = 3a\); \(AB = a\). Góc giữa mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\) bằng \({45^0}\). Tính thể tích khối chóp \(S.ABC\) theo \(a\).
- A \({V_{S.ABC}} = \frac{{4{a^3}}}{9}\).
- B \({V_{S.ABC}} = \frac{{{a^3}\sqrt 2 }}{6}\).
- C \({V_{S.ABC}} = \frac{{{a^3}\sqrt 2 }}{2}\).
- D \({V_{S.ABC}} = \frac{{2{a^3}}}{9}\).
Phương pháp giải:
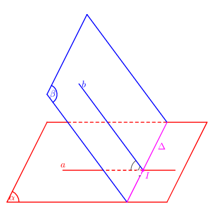
Xác định góc giữa hai mặt phẳng \(\left( \alpha \right),\,\,\left( \beta \right)\):
- Tìm giao tuyến \(\Delta \) của \(\left( \alpha \right),\,\,\left( \beta \right)\).
- Xác định 1 mặt phẳng \(\left( \gamma \right) \bot \Delta \).
- Tìm các giao tuyến \(a = \left( \alpha \right) \cap \left( \gamma \right),b = \left( \beta \right) \cap \left( \gamma \right)\)
- Góc giữa hai mặt phẳng \(\left( \alpha \right),\,\,\left( \beta \right)\): \(\left( {\widehat {\left( \alpha \right);\left( \beta \right)}} \right) = \left( {\widehat {a;b}} \right)\).
Lời giải chi tiết:
Kẻ \(AH \bot BC,\,\,\left( {H \in BC} \right)\)
Ta có: \(\left( {SBC} \right) \cap \left( {ABC} \right) = BC\)
\(BC \bot AH,\,\,BC \bot SA\,\,\left( {do\,\,SA \bot \left( {ABC} \right)} \right) \Rightarrow BC \bot \left( {SAH} \right)\)
\( \Rightarrow \left( {\widehat {\left( {SAC} \right);\left( {ABC} \right)}} \right) = \left( {\widehat {SH;AH}} \right) = \widehat {SHA} = {45^0}\)
\(\Delta ABC\) vuông tại \(A \Rightarrow AB = \sqrt {B{C^2} - A{C^2}} = \sqrt {{{\left( {3a} \right)}^2} - {a^2}} = 2\sqrt 2 a\) và
\({S_{ABC}} = \frac{1}{2}.AB.AC = \frac{1}{2}.2\sqrt 2 a.a = \sqrt 2 {a^2}\)
\(AH \bot BC \Rightarrow AH.BC = AB.AC \Rightarrow AH = \frac{{2\sqrt 2 a.a}}{{3a}} = \frac{{2\sqrt 2 a}}{3}\)
\(\Delta SAH\) vuông tại A, \(\widehat {SHA} = {45^0} \Rightarrow \Delta SAH\) vuông cân tại A \( \Rightarrow SA = AH = \frac{{2\sqrt 2 a}}{3}\)
Thể tích khối chóp \(S.ABC\): \(V = \frac{1}{3}.SA.{S_{ABC}} = \frac{1}{3}.\frac{{2\sqrt 2 a}}{3}.\sqrt 2 {a^2} = \frac{4}{9}{a^3}\).
Chọn: A