Câu hỏi
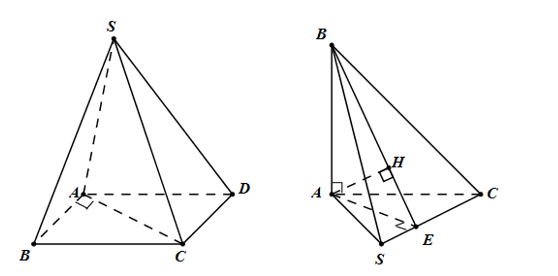
Cho hình chóp \(S.ABCD\) có đáy ABCD là hình bình hành thỏa mãn \(AB = a,\,AC = a\sqrt 3 ,\,BC = 2a\). Biết tam giác SBC cân tại S, tam giác SCD vuông tại C và khoảng cách từ D đến mặt phẳng \(\left( {SBC} \right)\) bằng \(\frac{{a\sqrt 3 }}{3}\). Tính thể tích V của khối chóp đã cho.
- A \(V = \frac{{2{a^3}}}{{3\sqrt 5 }}\).
- B \(\frac{{{a^3}}}{{3\sqrt 5 }}\).
- C \(V = \frac{{{a^3}}}{{3\sqrt 3 }}\).
- D \(\frac{{{a^3}}}{{\sqrt 5 }}\).
Phương pháp giải:
+) Chứng minh \(AB \bot \left( {SAC} \right) \Rightarrow {V_{S.ABC}} = {V_{B.SAC}} = \frac{1}{3}AB.{S_{\Delta SAC}}\).
+) \(AD//BC \Rightarrow d\left( {D;\left( {SBC} \right)} \right) = d\left( {A;\left( {SBC} \right)} \right)\)
+) Dựng \(AE \bot SC,\) tính AE.
+) Tính \(\cos C\) của tam giác SBC, từ đó tính SC, tính \({S_{\Delta SAC}} = \frac{1}{2}AE.SC\).
Lời giải chi tiết:
Ta có \(A{B^2} + A{C^2} = {a^2} + 3{a^2} = 4{a^2} = B{C^2} \Rightarrow \Delta ABC\) vuông tại A (Định lí Pytago đảo)
\( \Rightarrow AB \bot AC \Rightarrow CD \bot AC\,\,\,\left( 1 \right)\)
Mà \(CD \bot SC\,\,\,\left( 2 \right)\,\,(\Delta SCD\) vuông tại C)
Từ (1) và (2) \( \Rightarrow CD \bot \left( {SAC} \right) \Rightarrow AB \bot \left( {SAC} \right)\)
Ta có: AD // BC \( \Rightarrow AD//\left( {SBC} \right) \Rightarrow d\left( {D;\left( {SBC} \right)} \right) = d\left( {A;\left( {SBC} \right)} \right)\)
Dựng \(AE \bot SC\) tại E, \(AH \bot BE\) tại H ta có \(d\left( {A;\left( {SBC} \right)} \right) = AH = \frac{{a\sqrt 3 }}{3}\)
Ta có: \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{E^2}}} \Rightarrow \frac{3}{{{a^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{A{E^2}}} \Leftrightarrow AE = \frac{a}{{\sqrt 2 }}\)
\(BE = \sqrt {{a^2} + \frac{{{a^2}}}{2}} = \frac{{a\sqrt 6 }}{2}\)
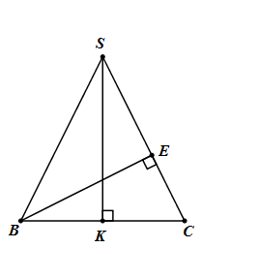
Xét tam giác vuông BCE: \(\sin C = \frac{{BE}}{{BC}} = \frac{{\frac{{a\sqrt 6 }}{2}}}{{2a}} = \frac{{\sqrt 6 }}{4} \Rightarrow \cos C = \frac{{\sqrt {10} }}{4}\)
Áp dụng định lí cosin ta có:
\(\begin{array}{l}\cos C = \frac{{B{C^2} + S{C^2} - S{B^2}}}{{2BC.SC}} = \frac{{B{C^2}}}{{2BC.SC}} = \frac{{BC}}{{2SC}}\\ \Rightarrow \frac{{\sqrt {10} }}{4} = \frac{{2a}}{{2SC}} \Leftrightarrow SC = \frac{{4a}}{{\sqrt {10} }}\end{array}\)
\( \Rightarrow {S_{\Delta SAC}} = \frac{1}{2}AE.SC = \frac{1}{2}.\frac{a}{{\sqrt 2 }}.\frac{{4a}}{{\sqrt {10} }} = \frac{{{a^2}\sqrt 5 }}{5}\)
\( \Rightarrow {V_{S.ABC}} = \frac{1}{3}AB.{S_{\Delta SAC}} = \frac{1}{3}.a.\frac{{{a^2}\sqrt 5 }}{5} = \frac{{{a^3}\sqrt 5 }}{{15}} \Rightarrow {V_{S.ABCD}} = 2{V_{S.ABC}} = \frac{{2{a^3}\sqrt 5 }}{{15}} = \frac{{2{a^3}}}{{3\sqrt 5 }}\)
Chọn đáp án A.