Câu hỏi
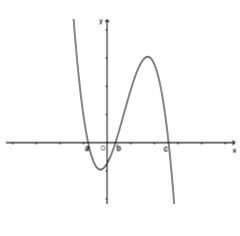
Cho hàm số \(y = f(x)\) có đồ thị \(y = f'(x)\) cắt trục Ox tại ba điểm có hoành độ \(a < b < c\) như hình vẽ.
Xét 4 mệnh đề sau:
\(\left( 1 \right):\,\,f(c) > f(a) > f(b).\)
\(\left( 2 \right):f(c) > f(b) > f(a).\)
\(\left( 3 \right):\,\,f(a) > f(b) > f(c).\)
\(\left( 4 \right):f(a) > f(b).\)
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng ?
- A 4
- B 1
- C 2
- D 3
Phương pháp giải:
Xác định các nghiệm của phương trình \(f'\left( x \right) = 0\) và xét dấu của \(f'\left( x \right)\), từ đó lập BBT của hàm số \(f\left( x \right)\) và kết luận.
Lời giải chi tiết:
Ta có \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = a\\x = b\\x = c\end{array} \right.\)
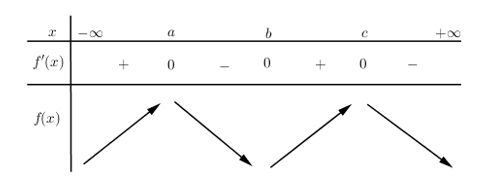
Lập BBT của đồ thị hàm số \(y = f\left( x \right)\) như sau:
Dựa vào BBT ta thấy chỉ có 1 mệnh đề đúng là \(f\left( a \right) > f\left( b \right)\).
Chọn đáp án B.
Câu hỏi trước
