Câu hỏi
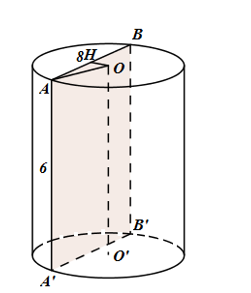
Cho khối trụ \(\left( T \right)\) có O và O’ là tâm hai đường tròn đáy. Gọi \(ABB'A'\) là thiết diện song song với trục \(OO'\) (A, B thuộc đường tròn O; A’, B’ thuộc đường tròn O’). Biết \(AB = 8,\,\,AA' = 6\) và thể tích của khối trụ \(\left( T \right)\) bằng \(150\pi \). Tính khoảng cách từ O đến mặt phẳng (ABB’A’).
- A \(d = 5\)
- B \(d = 2\)
- C \(d = 3\)
- D \(d = 4\).
Phương pháp giải:
+) Gọi H là trung điểm của AB \( \Rightarrow OH = d\left( {O;\left( {ABB'A'} \right)} \right)\).
+) Sử dụng công thức tính thể tích khối trụ \(V = \pi {R^2}h\).
Lời giải chi tiết:
Gọi H là trung điểm của AB ta có \(OH \bot AB \Rightarrow OH = d\left( {O;\left( {ABB'A'} \right)} \right)\).
Ta có \(\pi {R^2}h = 150\pi \Leftrightarrow \pi {R^2}.6 = 150\pi \Leftrightarrow R = 5 = OA\).
Xét tam giác vuông OHA: \(OH = \sqrt {O{A^2} - A{H^2}} = \sqrt {{5^2} - {4^2}} = 3\).
Vậy \(d\left( {O;\left( {ABB'A'} \right)} \right) = 3\).
Chọn đáp án C.
Câu hỏi trước
