Câu hỏi
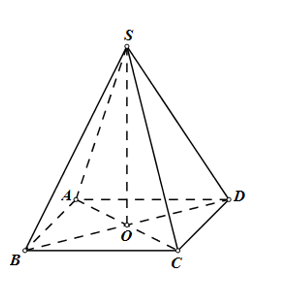
Cho khối chóp tứ giác đều S.ABCD có cạnh bên bằng 6, góc giữa đường thẳng SA và BC bằng 600. Tính thể tích V của khối chóp S.ABCD?
- A \(V = 36\)
- B \(V = 18\)
- C \(V = 36\sqrt 2 \)
- D \(V = 18\sqrt 3 \)
Phương pháp giải:
Gọi \(O = AC \cap BD \Rightarrow {V_{S.ABCD}} = \frac{1}{3}SO.{S_{ABCD}}\).
Lời giải chi tiết:
Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\)
Ta có: BC // AD \( \Rightarrow \widehat {\left( {SA;BC} \right)} = \widehat {\left( {SA;AD} \right)} = \widehat {SAD} = {60^0} \Rightarrow \Delta SAD\) đều \( \Rightarrow AD = SA = 6\)
\( \Rightarrow AC = 6\sqrt 2 \Rightarrow AO = \frac{{AC}}{2} = 3\sqrt 2 \)
Xét tam giác vuông SAO :
\(SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {{6^2} - {{\left( {3\sqrt 2 } \right)}^2}} = 3\sqrt 2 \)
\( \Rightarrow {V_{S.ABCD}} = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}.3\sqrt 2 {.6^2} = 36\sqrt 2 \)
Chọn đáp án C.