Câu hỏi
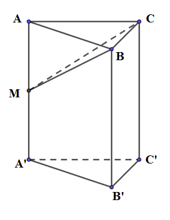
Cho khối lăng trụ \(ABC.A'B'C'\). Gọi \(M\) là trung điểm của \(AA'\). Mặt phẳng \(\left( {BCM} \right)\) chia khối lăng trụ \(ABC.A'B'C'\) thành hai khối. Tính tỉ số thể tích (số lớn chia số bé) của hai khối đó.
- A 6.
- B 3.
- C 4.
- D 5.
Phương pháp giải:
Lập tỉ lệ thể tích của hai khối trên với thể tích của khối lăng trụ \(ABC.A'B'C'\).
Lời giải chi tiết:
Đặt \({V_{ABC.A'B'C'}} = V\). Khi đó: \(\frac{{{V_{M.ABC}}}}{V} = \frac{1}{3}.\frac{1}{2} = \frac{1}{6} \Rightarrow {V_{M.ABC}} = \frac{V}{6}\)
\( \Rightarrow {V_{MBC.A'B'C'}} = V - \frac{V}{6} = \frac{{5V}}{6} \Rightarrow \frac{{{V_{MBC.A'B'C'}}}}{{{V_{M.ABC}}}} = \frac{{\frac{{5V}}{6}}}{{\frac{V}{6}}} = 5\).
Chọn: D