Câu hỏi
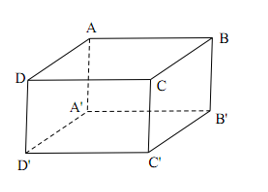
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có \(AB = a,\,AD = \sqrt 2 a,\,\,AC' = 2\sqrt 3 a\). Tính theo a thể tích V của khối hộp ABCD.A’B’C’D’.
- A \(V = 2\sqrt 6 {a^3}\).
- B \(V = \frac{{2\sqrt 6 }}{3}{a^3}\).
- C \(V = 3\sqrt 2 {a^3}\).
- D \(V = 6{a^3}\).
Phương pháp giải:
Thể tích khối hộp chữ nhật : \(V = abc\).
Lời giải chi tiết:
ABCD là hình chữ nhật \( \Rightarrow AC = \sqrt {A{B^2} + A{D^2}} = \sqrt {{a^2} + {{\left( {\sqrt 2 a} \right)}^2}} = \sqrt 3 a\)
ACC’A’ là hình chữ nhật \( \Rightarrow AA' = \sqrt {AC{'^2} - A{C^2}} = \sqrt {{{\left( {2\sqrt 3 a} \right)}^2} - {{\left( {\sqrt 3 a} \right)}^2}} = 3a\)
Thể tích khối hộp chữ nhật: \(V = AB.AD.AA' = a.\sqrt 2 a.3a = 3\sqrt 2 {a^3}\).
Chọn: C
Câu hỏi trước
