Câu hỏi
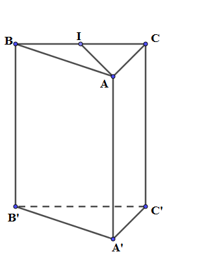
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân tại A, \(\widehat {BAC} = {120^0}\), \(BC = AA' = \sqrt 3 a\). Tính theo a thể tích V của khối lăng trụ ABC.A’B’C’.
- A \(V = \frac{{9{a^3}}}{4}\).
- B \(V = \frac{{3\sqrt 3 {a^3}}}{2}\).
- C \(V = \frac{{3\sqrt 6 {a^3}}}{6}\).
- D \(V = \frac{{3{a^3}}}{4}\).
Phương pháp giải:
Thể tích khối lăng trụ : \(V = Sh\), trong đó : \(S\) là diện tích đáy, h là chiều cao.
Lời giải chi tiết:
Tam giác ABC cân tại A, \(\widehat {BAC} = {120^0}\), gọi I là trung điểm của BC \( \Rightarrow \left\{ \begin{array}{l}AI \bot BC\\\widehat {BAI} = {60^0}\end{array} \right.\)
\(AI = \frac{{BI}}{{\tan {{60}^0}}} = \frac{{\frac{{\sqrt 3 a}}{2}}}{{\sqrt 3 }} = \frac{a}{2}\)
\( \Rightarrow {S_{ABC}} = \frac{1}{2}.AI.BC = \frac{1}{2}.\frac{a}{2}.\sqrt 3 a = \frac{{{a^2}\sqrt 3 }}{4}\)
Thể tích khối lăng trụ : \(V = {S_{ABC}}.AA' = \frac{{{a^2}\sqrt 3 }}{4}.\sqrt 3 a = \frac{{3{a^3}}}{4}\).
Chọn: D
Câu hỏi trước
