Phương pháp giải:

Số nghiệm của phương trình \({\left| x \right|^3} - 3{x^2} - {m^2} = 0\) bằng số giao điểm của đồ thị hàm số \(y = {\left| x \right|^3} - 3{x^2}\) và đường thẳng \(y = {m^2}\).

Phác họa đồ thị hàm số \(y = {\left| x \right|^3} - 3{x^2}\), từ đó nhận xét số giao điểm trên.

Lời giải chi tiết:

Số nghiệm của phương trình \({\left| x \right|^3} - 3{x^2} - {m^2} = 0\) bằng số giao điểm của đồ thị hàm số \(y = {\left| x \right|^3} - 3{x^2}\) và đường thẳng \(y = {m^2}\).

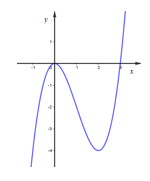
Từ đồ thị hàm số \(y = {x^3} - 3{x^2}\):

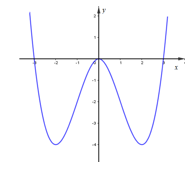
Ta vẽ được đồ thị hàm số \(y = {\left| x \right|^3} - 3{x^2}\) như sau:

Do \({m^2} \ge 0,\,\,\forall m\) nên đồ thị hàm số \(y = {\left| x \right|^3} - 3{x^2}\) cắt đường thẳng \(y = {m^2}\) tại nhiều nhất 3 điểm.

Chọn: B