Câu hỏi
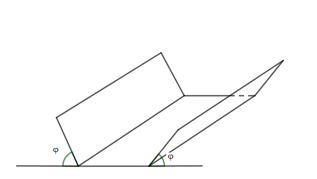
Bạn Nam làm một cái máng thoát nước mưa, mặt cắt là hình thang cân có độ dài hai cạnh bên và cạnh đáy đều bằng 20cm, thành máng nghiêng với mặt đất một góc \(\varphi \)\(\left( {{0^0} < \varphi < {{90}^0}} \right)\). Bạn Nam phải nghiêng thành máng một góc trong khoảng nào sau đây để lượng mưa thoát được là nhiều nhất?
- A \(\left[ {{{70}^0};{{90}^0}} \right)\).
- B \(\left[ {{{10}^0};{{30}^0}} \right)\).
- C \(\left[ {{{30}^0};{{50}^0}} \right)\).
- D \(\left[ {{{50}^0};{{70}^0}} \right)\).
Phương pháp giải:
Tính thể tích của khối lăng trụ đứng, có đáy là hình thang cân mà hai cạnh bên bằng đáy bé và bằng 20cm.
Thể tích lớn nhất khi diện tích của hình thang cân lớn nhất.
Lời giải chi tiết:
Thể tích nước lớn nhất khi diện tích của hình thang cân lớn nhất
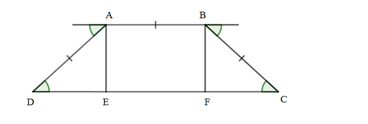
Gọi độ dài đường cao là h. Khi đó, \(AE = BF = h\), từ đó, suy ra \(DE = CF = \sqrt {{{20}^2} - {h^2}} = \sqrt {400 - {h^2}} \)
\(CD = DE + EF + FC = 2\sqrt {400 - {h^2}} + 20\)
Diện tích hình thang: \(S = \left( {AB + CD} \right).AE:2 = \frac{{20 + 2\sqrt {400 - {h^2}} + 20}}{2}.h = 20h + h\sqrt {400 - {h^2}} \)
\(S' = 20 + \sqrt {400 - {h^2}} - h.\frac{h}{{\sqrt {400 - {h^2}} }} = 20 + \frac{{400 - 2{h^2}}}{{\sqrt {400 - {h^2}} }}\)
\(S' = 0 \Leftrightarrow 20\sqrt {400 - {h^2}} + 400 - 2{h^2} = 0 \Leftrightarrow {h^2} = 300 \Rightarrow h = 10\sqrt 3 \)
Bảng xét dấu:
Diện tích hình thang lớn nhất khi \(h = 10\sqrt 3 \)
Khi đó, \(\sin \varphi = \frac{{10\sqrt 3 }}{{20}} = \frac{{\sqrt 3 }}{2} \Rightarrow \varphi = {60^0} \Rightarrow \varphi \in \)\(\left[ {{{50}^0};{{70}^0}} \right)\).
Chọn: D