Lời giải chi tiết:

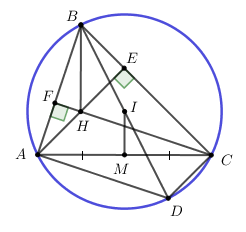
+) Gọi M là trung điểm của AC ta chứng minh \(\overrightarrow {BH}  = 2\overrightarrow {IM} \)

+) Nối \(BI \cap \left( O \right) = D \Rightarrow \widehat {BAD} = {90^0} \Rightarrow AD\parallel CH\) . Chứng minh tương tự ta cũng có: \(CD\parallel AH\)

Nên tứ giác ADCH là hình bình hành.

+) M là trung điểm của AC nên HD đi qua trung điểm M . Khi đó ta có MI là đường trung bình của tam giác BDH. \( \Rightarrow BH = 2IM \Rightarrow \overrightarrow {BH}  = 2\overrightarrow {IM} \)

+) \(\overrightarrow {BH} = 2\overrightarrow {IM} \Rightarrow \left( { - 2;2} \right) = 2\left( {{x_M} - 3;{y_M} + 3} \right) \Leftrightarrow \left\{ \begin{array}{l}{x_M} - 3 = - 1\\{y_M} + 3 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_M} = 2\\{y_M} = - 2\end{array} \right. \Rightarrow M\left( {2; - 2} \right)\)

\( \Rightarrow {\overrightarrow n _{AC}} = \overrightarrow {IM}  = \left( { - 1;1} \right)\)

Phương trình (AC): \( - 1\left( {x - 2} \right) + 1\left( {y + 2} \right) = 0 \Leftrightarrow  - x + y + 4 = 0\)

+) \(R = IB = \sqrt {{2^2} + {{\left( { - 4} \right)}^2}}  = 2\sqrt 5 \)

Phương trình đường tròn (C) là: \({\left( {x - 3} \right)^2} + {\left( {y + 3} \right)^2} = 20\)

+) Tọa độ của A, C là nghiệm của hệ phương trình : 

\(\begin{array}{l}
\left\{ \begin{array}{l}
- x + y + 4 = 0\\
{\left( {x - 3} \right)^2} + {\left( {y + 3} \right)^2} = 20
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = y + 4\\
{\left( {y + 1} \right)^2} + {\left( {y + 3} \right)^2} = 20
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
x = y + 4\\
2{y^2} + 8y - 10 = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = y + 4\\
\left[ \begin{array}{l}
y = 1\\
y = - 5
\end{array} \right.
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = - 1;y = - 5\\
x = 5;y = 1
\end{array} \right.
\end{array}\)

Do \({x_A} < {x_C}.\) nên \(A\left( { - 1; - 5} \right);C\left( {5;1} \right)\)

Chọn A.