Lời giải chi tiết:

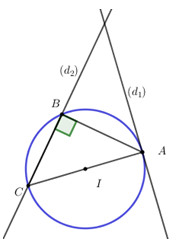
+) Vì \(A \in \left( {{d_1}} \right) \Rightarrow A\left( {a; - \sqrt 3 a} \right)\,\,,\left( {a > 0} \right)\)

+) Phương trình (AC) đi qua A và vuông góc với \(\left( {{d_1}} \right)\) là: \(x - \sqrt 3 y - 4a = 0\)

+) Tọa độ C là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}x - \sqrt 3 y - 4a = 0\\\sqrt 3 x - y = 0\end{array} \right. \Rightarrow C\left( { - 2a; - 2a\sqrt 3 } \right)\)

+) Phương trình (AB) đi qua A và  vuông góc với \(\left( {{d_2}} \right)\) là: \(x + \sqrt 3 y + 2a = 0\)

+) Tọa độ B là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}x + \sqrt 3 y + 2a = 0\\\sqrt 3 x - y = 0\end{array} \right. \Rightarrow B\left( { - \frac{a}{2};\frac{{ - a\sqrt 3 }}{2}} \right)\)

+) Ta tính được: \(AB = a\sqrt 3 ;BC = 3a \Rightarrow {S_{ABC}} = \frac{1}{2}AB.BC = \frac{1}{2}.a\sqrt 3 .3a = \frac{{\sqrt 3 }}{2} \Rightarrow a = \frac{1}{{\sqrt 3 }}\left( {do\,\,a > 0} \right)\)

Khi đó ta có: \(A\left( {\frac{1}{{\sqrt 3 }}; - 1} \right)\) và \(C\left( {\frac{{ - 2}}{{\sqrt 3 }}; - 2} \right) \Rightarrow I\left( { - \frac{1}{{2\sqrt 3 }}; - \frac{3}{2}} \right)\)

+) \(R = IA = \sqrt {{{\left( { - \frac{3}{{2\sqrt 3 }}} \right)}^2} + {{\left( {\frac{1}{2}} \right)}^2}}  = 1\)

Vậy phương trình đường tròn cần tìm là: \({\left( {x + \frac{1}{{2\sqrt 3 }}} \right)^2} + {\left( {y + \frac{3}{2}} \right)^2} = 1\)

Chọn D.