Lời giải chi tiết:

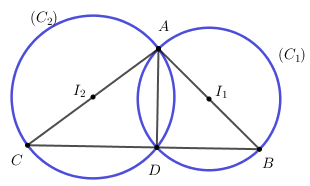
+) Giải hệ phương trình gồm \(\left( {{C_1}} \right);\left( {{C_2}} \right)\)ta tìm được tọa độ của A, D.

\(\begin{array}{l}
\left\{ \begin{array}{l}
{\left( {x + 1} \right)^2} + {y^2} = 10\\
{\left( {x - 5} \right)^2} + {\left( {y + 3} \right)^2} = 25
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{x^2} + 2x + 1 + {y^2} = 10\\
{x^2} + {y^2} - 10x + 6y + 9 = 0
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
12x - 6y - 18 = 0\\
{\left( {x + 1} \right)^2} + {y^2} = 10
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
2x - y = 3\\
{\left( {x + 1} \right)^2} + {y^2} = 10
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
y = 2x - 3\\
{\left( {x + 1} \right)^2} + {y^2} = 10
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
y = 2x - 3\\
{\left( {x + 1} \right)^2} + {\left( {2x - 3} \right)^2} = 10
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
y = 2x - 3\\
5{x^2} - 10x = 0
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = 2;y = 1\\
x = 0;y = - 3
\end{array} \right. \Rightarrow A\left( {2;1} \right);D\left( {0; - 3} \right)
\end{array}\)

+) A, D cố định nên số đo cung AD của 2 đường tròn là không đổi, suy ra 3 góc tam giác ABC không đổi.

Nên chu vi của tam giác ABC lớn nhất khi 1 cạnh lớn nhất.

+) Xét AB lớn nhất khi là đường kính của đường tròn. Nên I₁ là trung điểm của AB.

+) Đường tròn (C₁) có tâm \({I_1}\left( { - 1;0} \right);\,\,{R_1} = \sqrt {10} \), đường tròn (C₂) có tâm  \({I_2}\left( {5; - 3} \right);\,\,{R_2} = 5\)

+) Suy ra \(B\left( { - 4; - 1} \right)\) , tương tự \(C\left( {10; - 3} \right)\)

+) Phương trình đường thẳng BC là: \(\frac{{x + 4}}{{14}} = \frac{{y + 1}}{{ - 2}} \Leftrightarrow x + 4 =  - 7\left( {y + 1} \right) \Leftrightarrow x + 7y + 11 = 0\,\,\left( {BC} \right)\)

Chọn B.