Lời giải chi tiết:

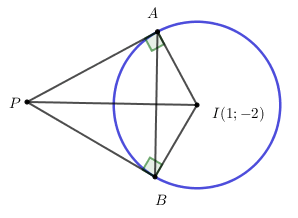
+) Ta có: \(I\left( {1; - 2} \right);R = 3\)

+) Tam giác PAB đều nên \(\widehat {APB} = {60^0} \Rightarrow \widehat {API} = {30^0}\)

\(\sin {30^0} = \frac{{AI}}{{PI}} \Rightarrow PI = \frac{{AI}}{{\sin {{30}^0}}} = \frac{3}{{\frac{1}{2}}} = 6\)

Suy ra P thuộc đường tròn (C’) tâm \(I\left( {1; - 2} \right);R' = PI = 6\)

Vậy phương trình đường tròn (C’) có dạng: \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 36\) 

Để có duy nhất điểm P thuộc (d) thì (d) phải tiếp xúc với (C’) 

\( \Leftrightarrow d\left( {I;d} \right) = R' \Leftrightarrow \frac{{\left| {3 + 8 + m} \right|}}{5} = 6 \Leftrightarrow \left| {11 + m} \right| = 30 \Leftrightarrow \left[ \begin{array}{l}
m = 19\\
m = - 41
\end{array} \right.\)

Chọn C.