Lời giải chi tiết:

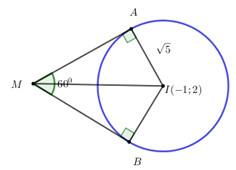
+) Ta có: \(I\left( { - 1;2} \right);R = \sqrt 5 \)

+) TH1: \(\widehat {AMB} = {60^0}\)

Tam giác AMI vuông tại A  có \(\widehat {AMI} = {30^0}\)(tính chất 2 tiếp tuyến cắt nhau)

\(\sin {30^0} = \frac{{AI}}{{MI}} \Rightarrow MI = \frac{{AI}}{{\sin {{30}^0}}} = \frac{{\sqrt 5 }}{{\frac{1}{2}}} \Rightarrow MI = 2\sqrt 5 \)

+) \(M \in \left( {C '} \right)\) tâm \(I\left( { - 1;2} \right);R' = MI = 2\sqrt 5 \)

Suy ra quỹ tích M là đường tròn (C’): \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 20\)

+) TH2: \(\widehat {AMB} = {120^0}\)

Tam giác AMI vuông tại A  có \(\widehat {AMI} = {60^0}\)(tính chất 2 tiếp tuyến cắt nhau)

\(\sin {60^0} = \frac{{AI}}{{MI}} \Rightarrow MI = \frac{{AI}}{{\sin {{60}^0}}} = \frac{{\sqrt 5 }}{{\frac{{\sqrt 3 }}{2}}} \Rightarrow MI = \frac{{2\sqrt 5 }}{{\sqrt 3 }}\)

+) \(M \in \left( {C ''} \right)\) tâm \(I\left( { - 1;2} \right);R'' = MI = \frac{{2\sqrt 5 }}{{\sqrt 3 }}\)

Suy ra quỹ tích M là đường tròn (C’): \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = \frac{{20}}{3}\)

Chọn B.