Câu hỏi
Cho đường tròn (C) có phương trình: \({x^2} + {y^2} + 4x - 2y + 1 = 0\) . Tử điểm \(M\left( {3;4} \right)\) kẻ hai tiếp tuyến MA, MB tới đường tròn (C) (A, B là 2 tiếp điểm). Tính AB.
- A \(AB = 2\sqrt 5 \)
- B \(AB = 4\sqrt 5 \)
- C \(AB = \frac{{4\sqrt {255} }}{{17}}\)
- D \(AB = \frac{{2\sqrt 5 }}{{13}}\)
Lời giải chi tiết:
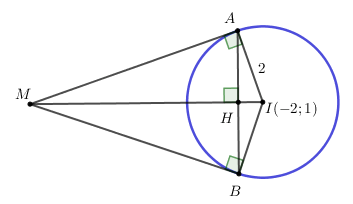
+) Ta có: tâm và bán kính của đường tròn lần lượt là: \(I\left( { - 2;1} \right);R = 2\) .
\(MI = \sqrt {25 + 9} = \sqrt {34} \)
+) Do MA là tiếp tuyến của đường tròn nên tam giác MAI vuông tại A. Ta có:
\(MA = \sqrt {M{I^2} - I{A^2}} = \sqrt {34 - 4} = \sqrt {30} \)
Gọi AB giao MI tại H khi đó ta có MI là trung trực của AB (tính chất 2 tiếp tuyến cắt nhau)
Áp dụng hệ thức lượng trong tam giác vuông MAI với AH là đường cao ta có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{M{A^2}}} + \frac{1}{{A{I^2}}} = \frac{1}{{30}} + \frac{1}{4} = \frac{{17}}{{60}} \Rightarrow AH = \frac{{2\sqrt {255} }}{{17}}\)
Ta có: \(AB = 2AH = \frac{{4\sqrt {255} }}{{17}}\)
Chọn C.







