Câu hỏi
Cho đường tròn (C) có phương trình \({x^2} + {y^2} - 8x - 4y - 16 = 0;M\left( { - 1;0} \right).\) Lập phương trình đường thẳng (d) đi qua M và cắt đường tròn (C) tại A, B để AB Min.
- A \(5x + 2y + 5 = 0.\)
- B \(x + 2y + 5 = 0.\)
- C \(5x + y + 5 = 0.\)
- D \(5x + 2y - 5 = 0.\)
Lời giải chi tiết:
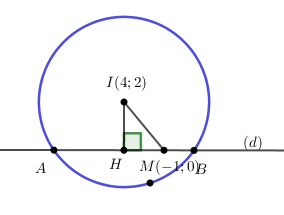
+) Nhận xét: điểm M nằm trong đường tròn (C)
+) Vẽ \(IH \bot \left( d \right) \Rightarrow IH \le IM \Rightarrow I{H_{{\rm{max}}}} = IM \Leftrightarrow M \equiv H\)
+) Nhận xét: \(I{H^2} + H{B^2} = {R^2}\) (không đổi)
\(\Rightarrow HB\,\,\min \Leftrightarrow IH\,\,\max \Leftrightarrow M\equiv H\)
\( \Rightarrow \left( d \right) \bot IM \Rightarrow {\overrightarrow n _d} = \overrightarrow {MI} = \left( {5;2} \right)\)
Phương trình đường thẳng (d) là: \(5\left( {x + 1} \right) + 2\left( {y - 0} \right) = 0 \Leftrightarrow 5x + 2y + 5 = 0.\)
Chọn A.
Câu hỏi trước
